Open Source AI and the Challenges Ahead

This essay was originally published as a blog post on Open Cybernetics & ChainlessCoder.
The price of AI
While I remain confident that open source AI will continue to bloom, I believe that the incentives for corporations and governments to limit access to novel neural network architectures and techniques will only intensify in the coming years. In this essay, I aim to predict and outline the potential disruptions that may occur over the course of this decade, and to offer some ideas and solutions to help the open source community adapt to this hypothetical future. Predicting the future is of course difficult, and I realize that many of the predictions I make may not come to pass or may unfold entirely differently. However, this does not render the exercise of thinking about the future futile. Rather, contemplating possible futures can help us adapt proactively to an ever-changing world. As our world continues to evolve at a rapid pace, the ability to envision and prepare for possible new worlds will become ever more important.
In the near future, the way we interact with people, the way we exchange and perform labor, even the way societies are organized will change in fundamental ways. It appears highly probable that each person will have personalized AI entities, which I refer to as “Ghosts”, that will link them to a global network of other AI systems. These AI systems will perform many services for us. Rather than perceiving them as mere assistants, it may be more fitting to regard them as cognitive extensions of ourselves. Firms and organizations will most likely also have their own Ghosts, enabling more effective collaboration among members. Beyond the social aspects, associative memory networks with recurrent connections might enable AI systems to form a memory. These stand-alone Ghosts might even develop an identity. Furthermore, AI systems leveraging consensus algorithms may be developed, potentially giving rise to decentralized autonomous AIs. Although this future has yet to materialize, we can already envision some of the economic dynamics that will unfold.
The exchange-value of AI-generated services will be equal to the energy required to provide the service (i.e. the cost of running the relevant model(s)), plus the AI’s information asymmetry within the market. Services that are relatively simple to replicate using AIs will inevitably have low exchange-values, leading to diminished surplus-value for the AI owners. This trend will particularly impact service-based economies, which can expect a significant reduction in surplus-value for most services. Consequently, we can expect that for a period, the populations and governments of many Western nations will react similarly to the Luddites of the 19th century. Driven by the diminished returns experienced across sectors, many regions of the world will resort to monopolistic licensing strategies and autocratic rules to impede AI access.
In more AI-progressive regions of the world, open source AI will most likely flourish for services with low exchange-value, but high use-value (i.e. services that are relatively simple to replicate using AI). However, for services where a small improvement in model performance can lead to a significant enhancement in use-value, the economic incentives will look very different. For this category of services, we can expect winner-take-all dynamics. More advanced AI systems will be able to extract significantly more surplus-value. As a result, the incentives to share innovations for techniques and model architectures will decline. Note however that the extraction of surplus-value in a system can only occur while there is an asymmetry between the participants of the system. In the context of AI, this asymmetry is likely to manifest itself in the form of information asymmetry, which involves controlling and limiting others from accessing information and knowledge.
Some of the information asymmetry between participants will be the result of government enforced restrictions (intellectual property, licensing, access control); this type of information asymmetry requires political action and can’t be solved through technology alone. Technology however can address information asymmetries resulting from resource asymmetries. To elaborate, today’s artificial neural networks are typically trained in a dense manner, meaning that once an input is provided, all units within the network get activated. For architectures like the Transformer (used in services like ChatGPT), the computational cost of propagating information is significantly higher, because of its “self-attention” step. High computational complexity leads to high energy consumption.
Because of the immense resources needed to train large language models (LLMs), we can expect that the development and management of AI systems for “winner-take-all” scenarios will start to cluster around a small group of close-sourced entities. These entities will be incentivized to maintain their model weights and architectures as proprietary, as increased secrecy leads to greater profitability. Resource limitations unfortunately also mean that for smaller entities such as researchers, non-profits, or startups, training LLMs from scratch is often not a viable option due to the high energy costs involved. As a result, most open source LLM efforts today rely on fine-tuning pre-existing models, which is cheaper and less energy-demanding. Because of these dynamics, I believe that one of the best things we can do to keep open source AI qualitatively competitive, is to reduce the costs associated with collectively training and running deep learning models at scale.
The Sparsely Activated Tensor
Taking into account the misaligned economic incentives, the energy consumption of densely trained LLMs, and the growing centralization of control, we at Open Cybernetics realized that a more proactive stance needs to be taken. Creating GPL-like standards for datasets will be an important step forward for the open source AI community. Nevertheless, we believe that copy-left licenses will not be enough to withstand the economic and political forces expected to emerge this decade. Instead, new technologies and protocols are needed for a shift in socioeconomic power-dynamics to occur.
I am particularly excited about a concept that we internally call “Sparsely Activated Tensor” and its synergy with the peer-to-peer space. Note, how we aim to build model agnostic Sparsely Activated Tensor data structures will be explored in future works. In this essay, my aim is simply to present the idea behind it, the rationale for developing this type of technology, and its implications for the open source community and beyond. A Sparsely Activated Tensor can be defined as a data structure that retrieves and updates its state in a sparse fashion. To better understand what is meant by this, let’s start with a simple example and build upon it.
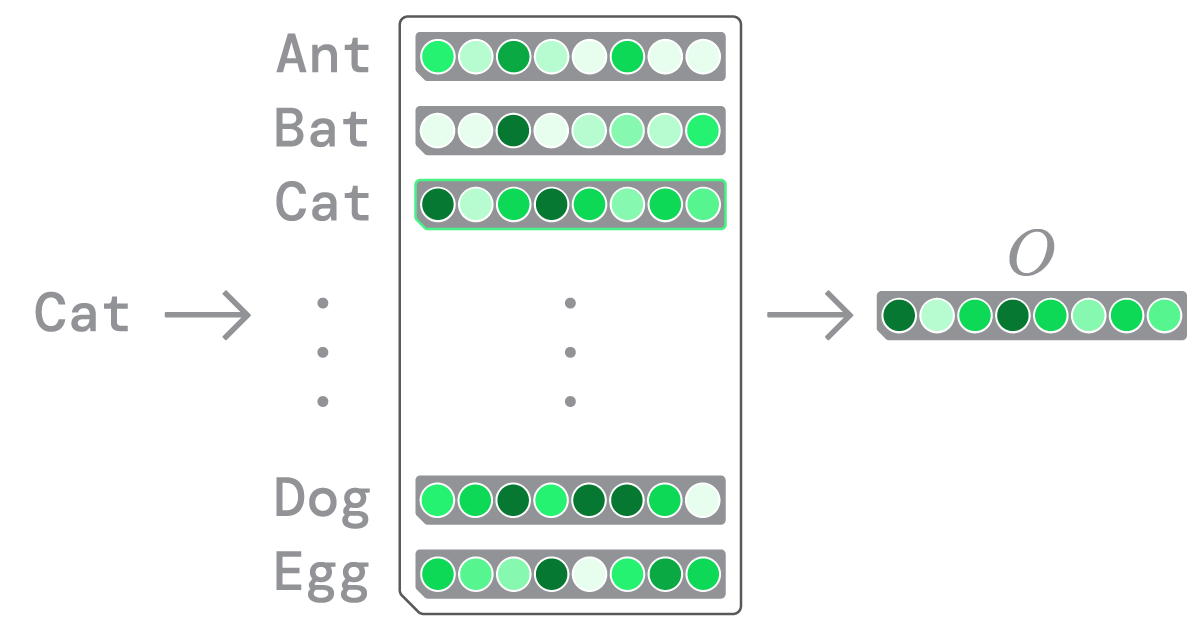
Figure 1
A depiction of an embedding layer.
An embedding layer can be viewed as a type of Sparsely Activated Tensor that operates on a one-to-one mapping principle. What that means: the embedding layer consists of a list of tokens (e.g. words), along with a weight matrix containing corresponding embeddings. Each word used in the corpus is assigned to one row in the weight matrix, creating a mapping of words to embeddings (see Figure 1). These embeddings then serve as input for a neural network. The reason why an embedding layer can be regarded as a Sparsely Activated Tensor is that it satisfies both criteria associated with such data structures:
-
The embeddings can be efficiently retrieved by employing a database, allowing for sparse retrieval without the need to load the entire tensor into memory.
-
The embeddings can be updated sparsely. During backpropagation through the embedding layer, only the weights associated with the used token(s) are adjusted, while the remaining embeddings are excluded from the update step.
While a one-to-one mapping approach proves valuable in situations involving discrete tokens like words, it is impractical in the case of continuous inputs. For example, a \(28 \times 28\) image patch contains an exceedingly large number of potential pixel combinations, rendering it impractical to use an embedding layer that relies on a one-to-one mapping. However, as we will see in a moment, using a many-to-one mapping approach allows us to achieve similar results. The logical connection between embedding retrieval and Sparsely Activated Tensors will become apparent in a moment.
Consider a scenario where we have a normalized matrix, \(W_K\), consisting of stored patterns, along with a normalized input, \(I\) (see Figure 2). Performing a dot product between \(I\) and \(W_K\) is essentially akin to examining each column of \(W_K\) and determining which column vector bears a closer resemblance to \(I\). The resulting \(K\) vector represents the cosine similarities between \(I\) and each column of \(W_K\). Higher scores within \(K\) indicate greater similarity between the input and the corresponding column.
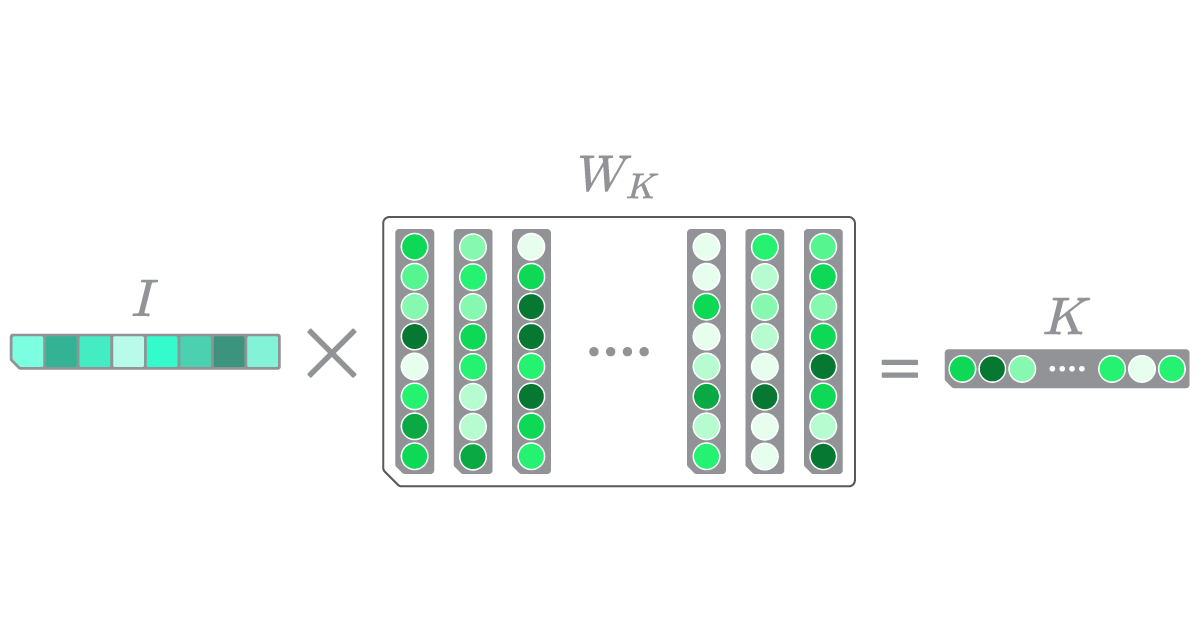
Figure 2
The values within \(K\) represent the similarity of \(W_k\)’s columns to \(I\)
By incorporating a softmax activation function, an additional weight matrix, \(W_V\), and a scalar parameter \(\beta\), for regulating the intensity of the softmax distribution, we are able to associate \(I\) with a given output \(O\) (see Figure 3). The resulting distribution from the softmax operation determines which rows of the \(W_V\) matrix will be given more importance. The configuration of this neural network layer is commonly referred to as a Modern Hopfield Lookup layer. It uses a weighted summation of a predetermined set of learnable patterns to establish an association between a continuous input and an output embedding.
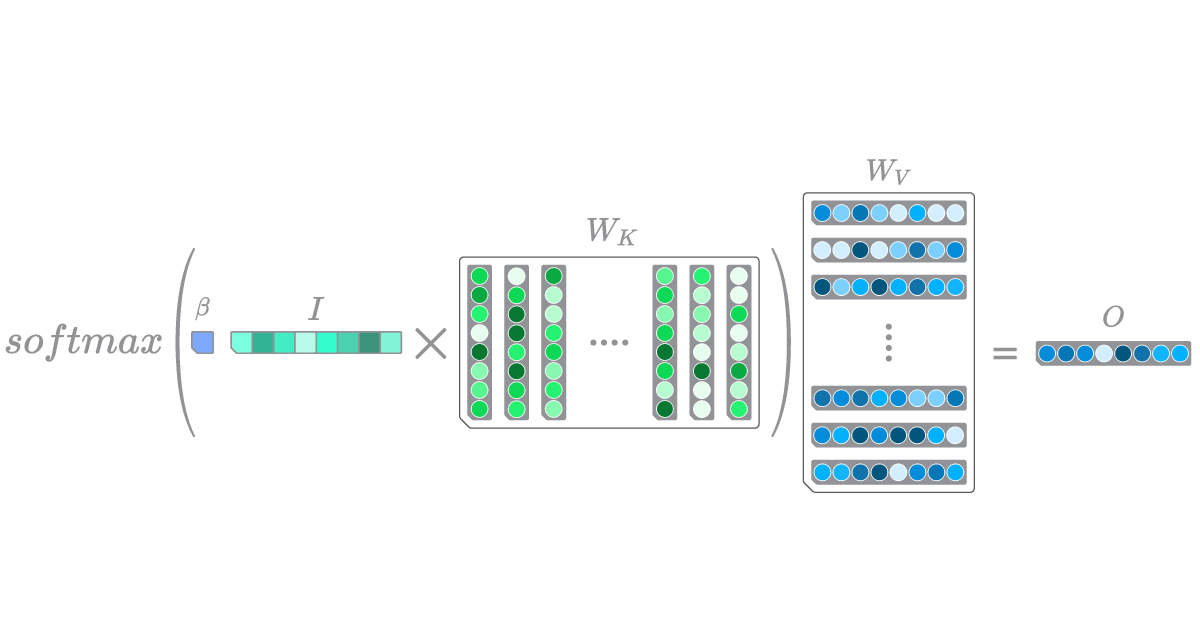
Figure 3
A depiction of a Modern Hopfield Lookup layer.
To some readers, it might be already evident that a considerable amount of computation is required to transition from \(I\) to \(O\). In the case of the self-attention step in Transformers, the computational demands are even more pronounced. As depicted in Figure 4., the self-attention step of a Transformer uses three matrices: the query (\(Q\)), key (\(K\)), and value (\(V\)) matrices, along with a softmax function. The presence of the \(\sqrt{d_k}\) term within the attention step serves a similar purpose as \(\beta\) does in the example depicted in Figure 3.
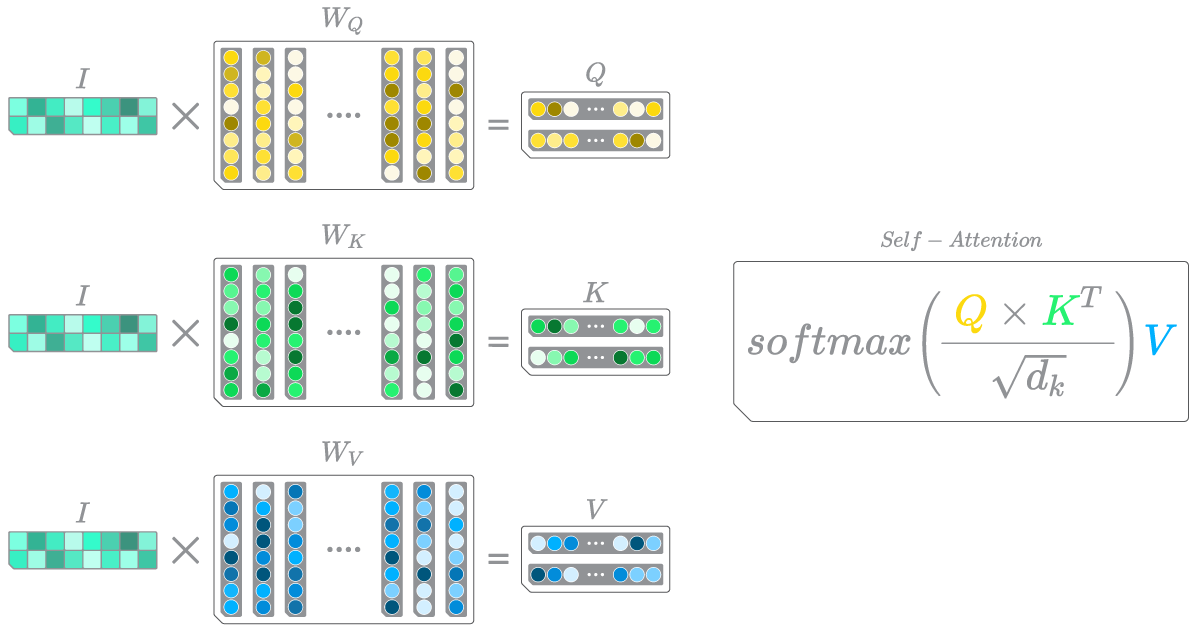
Figure 4
A depiction of the self-attention mechanism within Transformers. The multi-head component, as well as the layer normalization and residual connections of the encoder have been omitted for the sake of simplicity.
To derive the query, key, and value matrices, a substantial number of unnecessary cosine similarities need to be computed. To elaborate, a large portion of these dot products do not significantly contribute to the output embedding of the self-attention step. In other words, the majority of values within \(Q\), \(K\), and \(V\) tend to be significantly smaller than one. Despite this, the comparison between input \(I\) and all the columns of \(W_Q\), \(W_K\), and \(W_V\) is performed because the specific internal patterns of the weight matrices that yield the highest cosine similarities are unknown in advance. This lack of prior knowledge contributes to the computational cost associated with training Transformers, as we end up having to perform a dot product between the entire \(Q\) and \(K\) matrices.
To highlight the inefficiency of the information retrieval process in current AI systems, let’s consider a scenario where we have a large database and wish to execute a simple query. Presently, the operation of AI systems involves loading and iterating through the entire database in memory to retrieve a handful of matches that align with our query, instead of leveraging indexed records. As we can see, the current way that we propagate information through an associative memory network like the Transformer is highly inefficient. There are two potential ways to address this problem. One option is to use a machine learning approach by trying to modify the attention mechanism, with the goal of reducing its computational demands. This has been explored in projects such as Linformer and Performer. Alternatively, we can consider incorporating design principles from database systems without making alterations to the underlying model architecture.
We know for example that it is possible to perform an efficient approximate k-nearest neighbor (kNN) lookup between \(I\) and the weight matrices, without having to load or iterate through the entire tensor. Using such an approach results in a significant reduction in the computational demands of LLMs while conserving a substantial amount of energy. Interestingly, some LLMs are already using such techniques to some degree. For instance, the Memorizing Transformer utilizes an external memory by efficiently performing an approximate kNN lookup over a vector database. LLM implementations that leverage vector databases usually use the HNSW algorithm in the background.
Drawing an analogy to databases, the concept of “sparse retrieval” can be likened to having pre-indexed weights that enable record retrieval (i.e. stored patterns) without the need to iterate over the entire database. However, existing Transformer implementations that leverage vector databases are currently limited to performing approximate kNN lookups exclusively during inference. In other words, model training continues to be conducted in a dense manner, which is an energy intensive process. In order to facilitate the collective training of large-scale neural networks, a shift is required from updating model weights simultaneously to updating them sparsely. By designing neural building blocks that embrace sparse retrieval and sparse update, we can contribute to the empowerment of the open-source AI community in overcoming the information asymmetry caused by resource limitations.
Cryptographic Ghost Proofs
As a strategy to mitigate resource constraints, some researchers within the open source AI community have already started to leverage trusted peer-to-peer collaboration for inference and fine-tuning of LLMs. For instance, projects like Petals are using Kademlia-based distributed hash tables to propagate neural activity across a decentralized network of nodes. This approach allows Petals users to distribute training and inference tasks among multiple nodes instead of relying on a single machine to load the entire LLM. By contributing collectively to the training process, these distributed nodes expand their capabilities beyond what they could achieve individually.
Despite the remarkable utility of these systems, current peer-to-peer AI efforts lack one critical component: trustlessness in an adversarial environment. Currently, if someone performs a forward pass in systems like Petals, you still have to trust other nodes within the network. That is, any malicious node can return an output that did not in fact originate from the model. While this limitation may not be the end of the world for collaborative academic endeavors, it does impede the widespread adoption of peer-to-peer AI systems in real-world applications.
And it is here where the second significant advantage of Sparsely Activated Tensors comes into play. In addition to their energy efficiency, Sparsely Activated Tensors have the necessary attributes to enable cryptographically secure forward and backward propagation within peer-to-peer AI networks. Now, let’s briefly examine the Merkle tree data structure to understand how such a feat is achievable.
A Merkle tree is a binary tree data structure used to securely verify the presence of values in a list, without having to provide every value of the list to another party. To create a Merkle tree, each value in the list is hashed using a cryptographic hash function, resulting in leaf nodes. These leaf nodes are then combined through hashing to form non-leaf parent nodes. This process is repeated until the root of the binary tree is reached (see Figure 5).
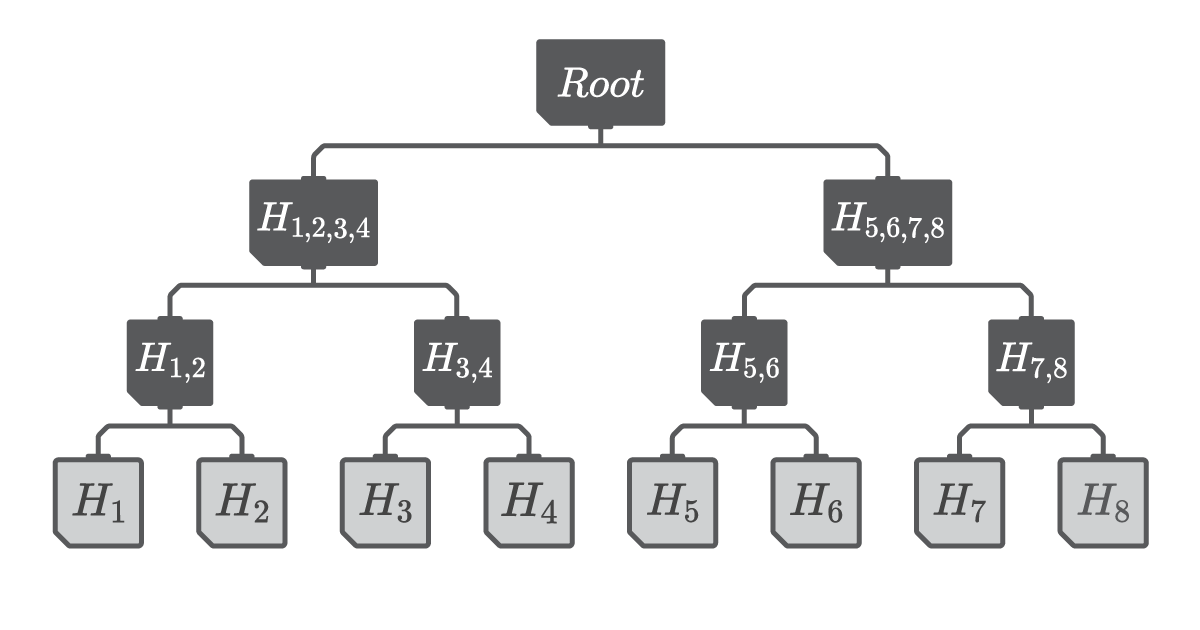
Figure 5
A depiction of a Merkle Tree. Leaf nodes are represented in gray.Non-leaf nodes are represented in black.
To confirm the presence of a value in the Merkle tree, a Merkle proof is used, consisting of a sequence of hashes. By iteratively hashing the leaf node hash with the provided Merkle proof, the original Merkle root can be reconstructed (see Figure 6). It is important to note that recipients of the Merkle proof must already possess a local copy of the Merkle root in order for the verification process to occur. By comparing the locally stored Merkle root with the final hash generated by the provided Merkle proof, a recipient node can verify if a value was included in the list of values used to create the Merkle root. If the two hashes match, it confirms that the provided value was indeed one of the leaf nodes in the original Merkle tree. Notice that the size of a Merkle proof (represented by green hashes within Figure 6) scales logarithmically. This allows us to provide compact presence proofs even if the number of leaf-nodes is large.
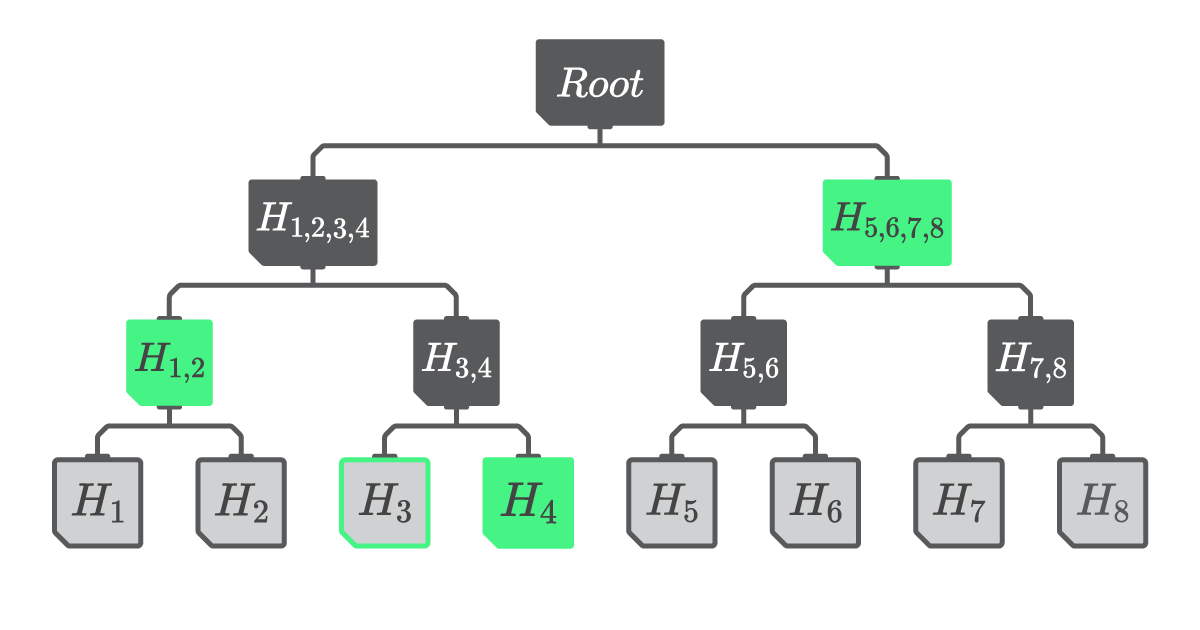
Figure 6
A depiction of a Merkle proof. To prove that \(H_3\) was present in the initial value list, one has to hash it with \(H_4\), then with \(H_{1,2}\), and finally with \(H_{5,6,7,8}\) (shown in green) to recreate the hash of the Merkle root.
The connection between the Merkle tree data structure and Sparsely Activated Tensors lies in their potential combination. A Merkle tree can be constructed on top of a Sparsely Activated Tensor, which retrieves and updates its state in a sparse manner. In this particular example, the column vectors of the tensor are used as leaf nodes in the Merkle tree (see Figure 7).
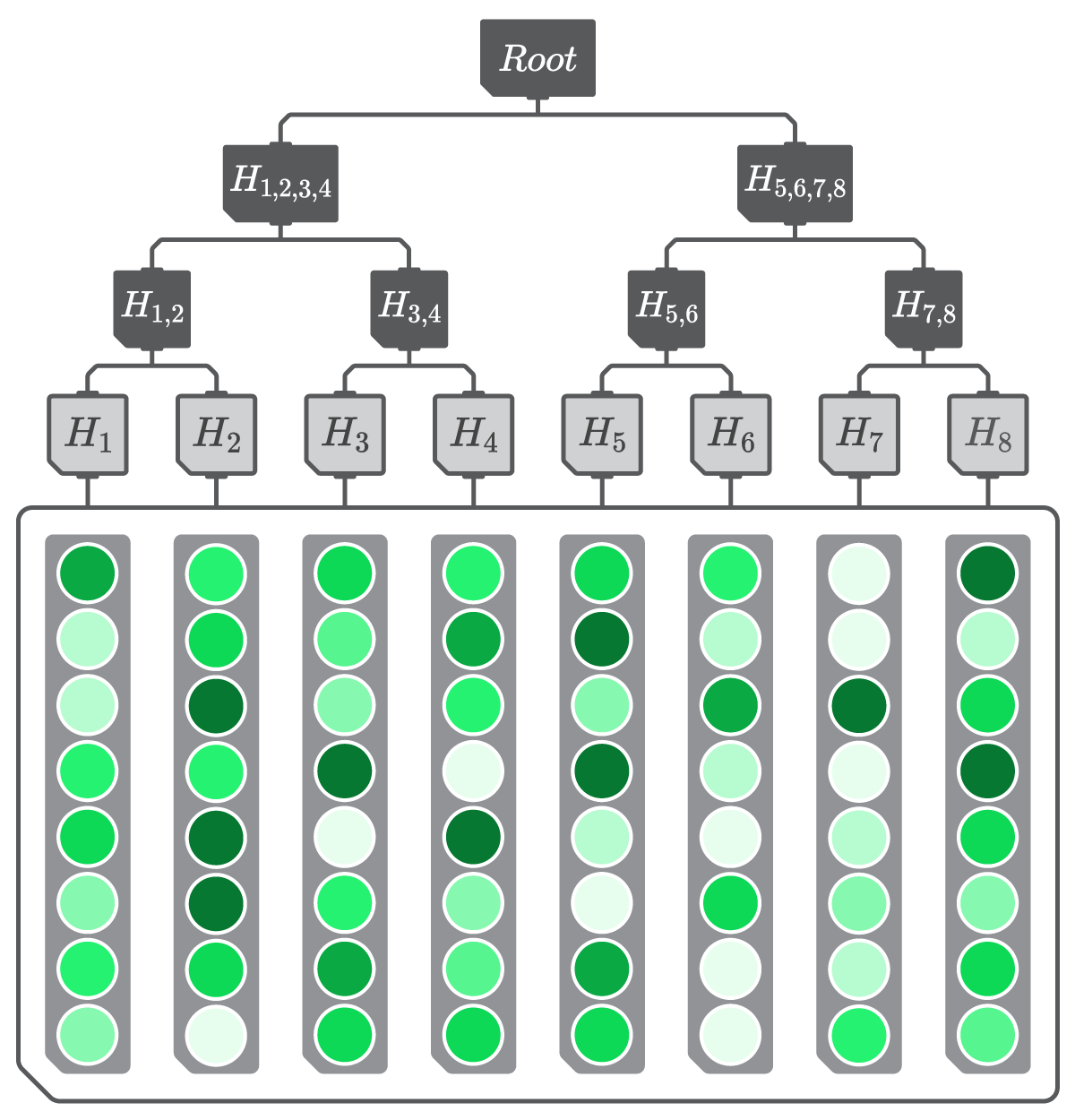
Figure 7
A depiction of a Merkle tree constructed using the columns of a Sparsely Activated Tensor as leaf nodes.
Let’s consider a scenario where Bob has a Modern Hopfield network with Hopfield Lookup layers (as in Figure 3). On the other hand, Alice holds a local copy of Bob’s Hopfield Lookup layer’s Merkle roots. Suppose Alice wants to send an input to Bob for performing forward propagation. Bob proceeds with a forward pass, which is equivalent to performing an approximate kNN lookup within the Sparsely Activated Tensor. Subsequently, Bob shares with Alice the \(k\) nearest column vectors from \(W_K\), along with \(W_K\)’s Merkle proof, as well as the corresponding vectors from \(W_V\), along with \(W_V\)’s Merkle proof (see Figure 8).
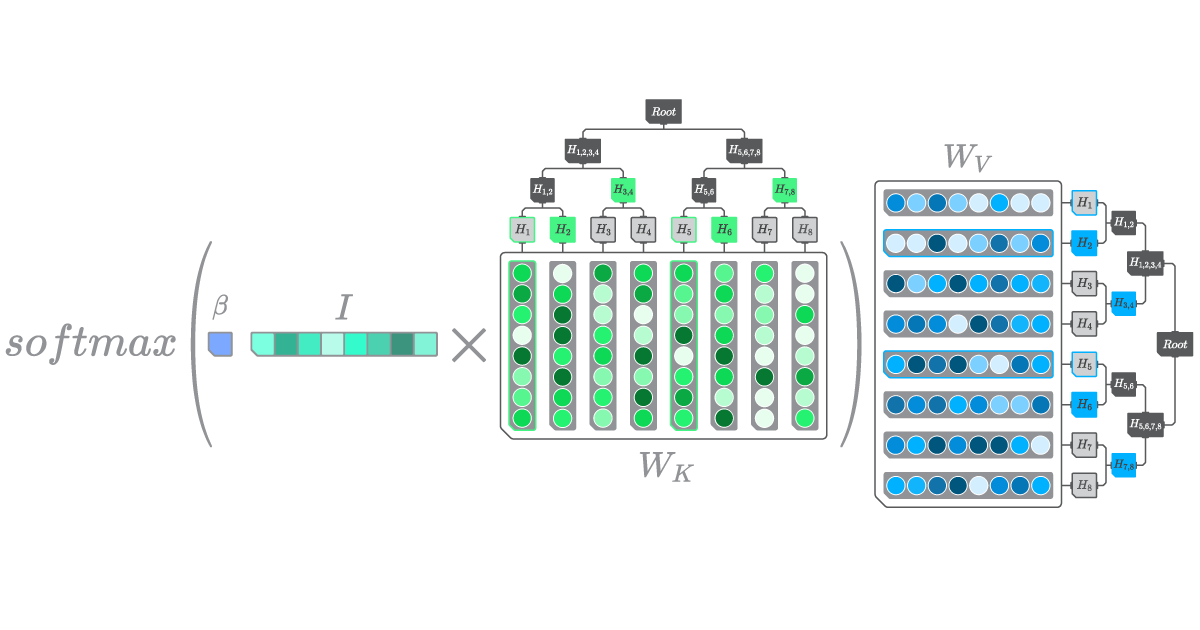
Figure 8
A depiction of a Cryptographic Ghost Proof for a Modern Hopfield Lookup layer. Let’s assume that the \(k\) nearest neighbors of \(I\) within \(W_K\) are the columns that resulted in \(H_1\) and \(H_5\). By hashing \(H_1\) with \(H_2\), \(H_5\) with \(H_6\), and then those generated hashes with \(H_{3,4}\) and \(H_{7,8}\), We can generate the Merkle root of the sparse scoring tensor. The same steps can then be performed to generate the Merkle root of \(W_V\).
Using the sparsely retrieved \(W_K\) and \(W_V\) embeddings, along with the provided Merkle proofs, Alice can generate a cryptographically verifiable output. It’s important to note that in a real-world implementation, Bob wouldn’t transmit the embeddings in an uncompressed format. Instead, he would employ delta encoding to compress the embeddings, significantly reducing the required bandwidth. Additionally, Bob wouldn’t send individual Merkle proofs for each \(k\) nearest column / row vector in \(W_K\) and \(W_V\). Instead, he would transmit a single Compact Merkle Multiproof for \(W_K\) and another for \(W_V\). Notice that the same technique can be applied within the self-attention step of the Transformer, assuming that Sparsely Activated Tensors are used.
At Open Cybernetics, We refer to Merkle Multiproofs for Sparsely Activated Tensors as Cryptographic Ghost Proofs (CGPs). We believe that CGPs can serve as a powerful building block and will play a significant role in future AI systems. Ghost proofs are also the reason why I believe that in the near future, the majority of internet traffic will be comprised of neural activity. With the existence of a "Ghost file" for every AI system, containing the Ghost roots for each network layer, along with architectural information and the operations involved in forward and backward propagation, entities can have absolute confidence that the outputs of AI systems originate solely from the model.
The use of CGPs and Ghost Files would not only introduce a new paradigm for peer-to-peer AI systems but also foster a culture of increased transparency. By incorporating Cryptographic Ghost Proofs into Internet protocols for AI interactions, the concealment of model architectures and weights would no longer be feasible. Ghost files would ensure transparency of model architectures, while CGPs would make model weights public (as a small part of the weights would be shared in a compressed form every time a forward pass is performed). This technological shift would enable artificial cognition to become a shared resource, accessible to all and owned by the people.
Reflection
In addition to openness and trustlessness, the integration of CGPs has the potential to merge the realms of AI and decentralized ledger technology, paving the way for the emergence of Autonomous AI systems. An Autonomous AI system is a peer-to-peer AI protocol that leverages the permissionless nature of consensus algorithms. Rather than changing entries in a ledger, these protocols would propagate thoughts. To ensure effective operation and prevent DoS attacks, these protocols would likely rely on mutual credit or a currency. The technical intricacies, as well as the economic and social ramifications of these autonomous systems will be explored in future works.
As engineers and AI researchers, we must recognize the inherent political nature of technology. Seemingly small engineering decisions can lead to profound social transformations. For instance, densely activated deep learning models can lead to centralized forms of social organization. While sparsely activated deep learning models can lead to decentralized forms of social organization. Now more than ever, we need to think across disciplines. For instance, it is worth considering the implications of decentralized AI on governance. How will AI systems impact nation states? Will they empower autocracies or contribute to the development of enhanced democracies? How about company organizational structure and minimum viable size? It is intriguing to imagine the possibility of creating scalable direct democracies by connecting each citizen’s personal Ghosts to a shared network. These ideas warrant further exploration in the future.
I hope that this essay will spark your interest in exploring the synergy between AI and peer-to-peer technology. I have strong confidence that significant advancements will unfold in the coming years at the intersection of AI and database systems, particularly in the realm of Sparsely Activated Tensors. Moreover, the convergence of AI and peer-to-peer systems, alongside the development of sparsely activated associative memory networks, will undoubtedly witness remarkable progress. I encourage you to explore these captivating topics and contribute to open source AI. Remember, the Free Libre Open Source movement is more than about sharing code. It is about empowering communities worldwide.